Rechercher une actualité Dernières actualités
Résoudre un problème de mathématiques avec la pédagogie PNL
Résoudre un problème de mathématiques avec la pédagogie PNL permet une réelle mise en situation et ainsi générer un scénario pour sortir du dialogue interne. Rappelons qu'en pédagogie active, le dialogue interne est un processus bloquant qui efface toute perspective de compréhension d'un sujet de mathématique ou autre branche.
Nous allons présenter ci-dessous un problème d'une classe de 11ème Harmos (classe de 3ème française) avec son énoncé initial puis la reformulation en vue de créer un scénario.
L’énoncé initial
Martin organise une Tombola. L’achat de 3000 € revient à 3400 €. En mettant le billet à 3€, il perdrait autant qu’il gagnerait en le mettant à 5€. Quel est le nombre de billet vendu ?
La reformulation avec la PNL d’apprentissage
Martin organise une Tombola. Il dépense pour les lots de la Tombola la somme de 3400€. On nous pose une devinette : combien de billet doit- il vendre pour que le montant de ses bénéfices en mettant chaque billet au prix de 5€ soit le même montant de ses pertes s’il mettait le billet au prix de 3€.
Les notions à connaître
- Pour résoudre ce type de problème : les équations (11h–3ef).
- Rappel de la définition d’une équation : une équation est une opération exprimée sous la forme d’une égalité dans laquelle se trouvent des inconnues.
- Notions acquises antérieures à contrôler : Le calcul littéral, simplification d'une expression.
La construction du scénario visuel
- Je visualise mentalement (visuel remémoré en PNL d’apprentissage) cette égalité avec la balance : d’un côté de la balance, j’ai un montant qui correspond aux pertes, de l’autre côté de la balance j’ai le même montant qui correspond aux gains (bénéfice)
-
Je définis ce qu'est une perte et un gain :
P = Dépenses - Recettes - G = Recettes - Dépenses - Je pose l'égalité comme le montre la balance : Perte = Gain
Pour notre problème, cela signifie :
Perte = 3400€ - (x billets à vendre à 3€) <=> 3400 - 3x
Gain = (x billets à vendre à 5€) - 3400€ <=> 5x - 3400
Si Perte = Gain alors 3400 - 3x = 5x - 3400
Je sors de la PNL pour résoudre de façon traditionnelle cette équation
- 3400 - 3x = 5x - 3400 [je pose l'équation de façon claire]
- 6800 = 5x + 3x [j'applique la règle des neutralisations des membres d'une opération]
- 6800 = 8x [je résouds partiellement mes opérations]
-
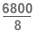= x = 850 [Je trouve l'inconnue x]
Vérification et conclusion
- En vendant 850 billets, je constate que si la vente de chaque billet est à 3€, je perds autant que je gagne si je vends le billet à 5€
- Gain : 850 billets x 5€ = 4250€ - 3400€ = 850€
- Perte : 850 billets x 3€ = 2550€ - 3400€ = -850€
CONTACT LAISSER UN COMMENTAIRE SUIVRE LA DISCUSSION (2 avis) POSTE par EDU-COACHING
Rédigé par anonyme
Bonjour, Mon fils à 13ans et en division spécialisée. est-ce que vous stages s'adressent aussi aux enfants de cette section?